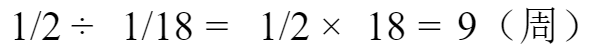牛吃草问题,也就是有名的牛顿问题,是牛顿的《普遍的算术》中提到的一道经典问题:12头牛4周吃草3格尔,同样的牧草21头牛9周吃10格尔。问24格尔牧草多少头牛18周能吃完(格尔为牧场面积单位)?其实质是一道“消长”问题。
牛吃草问题典型的特点隐含在建模之中:随着时间的推移,草的总量在不断地增加。草的总量包含两部分,一部分是原有草量,属于不变量;另一部分是新生长的草量,随着时间的推移在不断地增加。另外,模型中还要假设两个不变量:一是每头牛每天的吃草量是不变的,二是草每天生长的速度不变。
这样做的目的其实是为了简化问题。就像初中学习直线运动,统统都简化为匀速直线运动,到了高中基本模型就变成了匀变速直线运动,到了大学,运动问题直接应用微积分的相关知识处理。从这个角度去分析,实际上我们现在要说的是最简单的牛吃草问题,毕竟科学是逐步逼近真实,但永远到达不了真实,这也给科学家研究自然现象带来了无尽的兴趣。
一、应用算术的思维方法解决问题
牛吃草作为一个基本的数学模型,我看了很多辅导的视频,其实他们除了没有考虑每个孩子的认知水平不同外,对于问题的阶梯式设置还是很好的。具体做法是:先将牛限制在一片草地上吃草,这样就在很大程度上减少了变化量,使得问题有了层次感,孩子思考起来也就相对来说简单了很多,这也是我采用的方法。
例题:有一片牧场,牧草每天匀速生长,这片牧草可供24头牛吃6周,18头牛吃10周,问可供19头牛吃几周?
解法一:
具体解法是:先假设每头牛每周吃草量为1份,可按照不变量分成三个步骤:
1、先求牧场平均每周生长的牧草量,也就是新牧草的生长速度,属于不变量
草的生长速度等于(对应牛的头数乘以吃的较多的周数减去相应的牛的头数乘以吃的较少的周数)除以(吃的较多的周数减去吃的较少的周数),文字叙述总是复杂,列式计算就比较直观了。
列式计算:
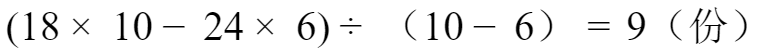
2、再求原有草量,等于牛头数乘以吃的周数减去草生长的速度乘以周数
列式计算:
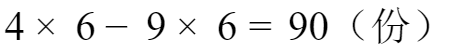
3、最后求19头牛吃草的周数
19头牛每周要吃19份草,每周生长的牧草量是9份,将19头牛分成两组:一组专门吃新生长的牧草,需要9头牛;剩余的10头吃原有草,这样就可以很巧妙地计算出来周数。
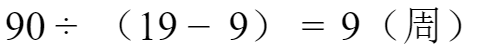
解法二:利用两种牛吃草方法做出示意图
从两种吃法中就可以看出:多出的草量是4周生长的牧草的份数,进而参照解法1将题目解答出来。
解法二的意义并不仅仅做出示意图,解出来题目,如果将牛放到示意图的左端,将新生草放到原有草量的右端,这道题目其实就可以变成同时不同地的两个物体的追击问题,这将对于孩子在初中乃至于高中的物理学科的学习帮助是很大的。
解法三:19头牛每周要吃19份草,先让19头把每周生长的9份新生草吃完,这样他们是吃不饱的,然后大家一起每周需要分享原有草为:
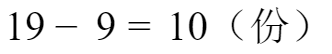
则原有草可供吃的天数为:

这几种解法里有些算式虽然相同,但是思维过程却不尽相同,这大致就是这些经典题目中蕴含的数学思维的美妙之处吧。
解法四:应用分数解决
步骤如下:第一步先求出来牧场平均每周生长的草量,即牧草的生长速度(不变量)
把18头牛吃10的周草的总量看作是“1”,平均每头牛每周吃了单位“1”的
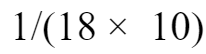
,这样,24头牛6周吃草的总量是:
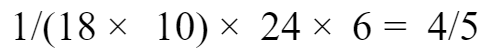
比单位“1”少了:
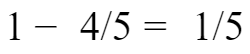
,少的这些的原因是牧草少生长了4周,说明少的
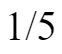
就是这个牧场4周的新长的草量,则牧场平均每周新生的草量为:
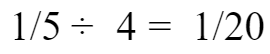
第二步:求牧场的原有草量(不变量)
从第一步的假设就可以看出来:单位“1”的总草量包括了原有草量和10周的新生草量。由于每周新生草量是单位“1”的
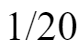
,所以10周的新生草量为单位“1”的
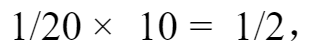
,则原有草量就是:
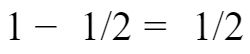
第三步:求这个牧场可供19头牛吃几天
19头牛每周的吃草量为:
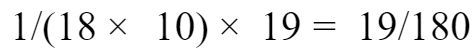
去掉每周的新生草量的
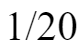
,19头牛每天还要从原有草量中吃掉:
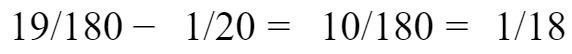
也就是说19头牛只要每周吃掉原有草量的
,不足部分从新生草量中补足,所以原有草量可供19头牛每周消耗的天数就是所要求的天数: